우선순위 큐 - Heap
일반적인 큐(Queue)는 First in-First Out 구조로 먼저 들어온 데이터가 먼저 나가는 구조였다. 하지만 우선순위 큐(Priority Queue)는 들어간 순서에 상관없이 우선순위가 높은 데이터가 먼저 나오는 것 것을 말한다. 우선순위 큐는 힙(Heap)이라는 자료구조를 가지고 구현할 수있기 때문에 이 둘을 묶어서 같이 쓴 것이다.
# 우선순위큐가 힙을 사용하는 이유 (알아두면 나쁠거 없음)
[주의] 왜 우선순위 큐는 배열이나 연결리스트로 구현하지 않을까? (출처 : 자료구조 - 우선순위 큐(Priority Queue)와 힙(heap) | ChanBLOG (chanhuiseok.github.io))
(1) 만일 배열로 구현한다고 가정합니다. 우선순위가 높은 순서대로 배열의 가장 앞부분부터 넣는다면, 우선순위가 높은 데이터를 반환하는 것은 맨 앞의 인덱스를 바로 이용하면 되므로 어렵지 않습니다.
하지만 우선순위가 중간인 것이 들어가야 하는 삽입 과정에서는 뒤의 데이터까지 인덱스를 모두 한 칸씩 뒤로 밀어야 하는 단점이 있습니다.
최악의 경우 삽입해야 하는 위치를 찾기 위해 모든 인덱스를 탐색해야 합니다. 즉 이 때의 시간 복잡도는 자료가 n개라고 할 때 O(n) 이 됩니다. → 배열로 구현 시 시간 복잡도 : 삭제는 O(1), 삽입은 O(n)
(2) 만일 연결리스트로 구현한다고 가정합니다. 이 또한 우선 순위가 높은 순서대로 연결을 시키면, 우선순위가 높은 데이터의 반환은 배열과 마찬가지로 쉽습니다.
하지만 연결리스트 또한 삽입의 과정 또한 배열과 마찬가지로 그 위치를 찾아야 합니다. 최악의 경우 맨 끝에까지 가게 됩니다. → 연결리스트로 구현 시 시간 복잡도 : 삭제는 O(1), 삽입은 O(n)
(3) 우선순위 큐를 힙으로 구현한다고 가정합니다. 힙의 경우 삭제나 삽입 과정에서 모두 부모와 자식 간의 비교만 계속 이루어집니다. (아래에서 다룰 것입니다)
즉, 이진 트리의 높이가 하나 증가할 때마다 저장 가능한 자료의 갯수는 2배 증가하며, 비교 연산 횟수는 1회 증가합니다. 즉 삭제나 삽입 모두 최악의 경우에는 O(log2n) 의 시간 복잡도를 가집니다. → 힙으로 구현 시 시간 복잡도 : 삭제는 O(log2n), 삽입은 O(log2n)
이처럼 배열이나 연결 리스트가 삭제에서는 시간 복잡도의 우위를 점할지라도, 삽입의 시간 복잡도가 힙 기반이 월등하기 때문에, 편차가 심한 배열과 연결리스트보다는 힙으로 구현하는 것입니다.
우선순위 큐
힙 자료구조는 트리 기반 구조로 자료가 순차적으로 저장되는 개념이 아니므로 비선형 자료구조를 가지게 된다.
힙은 완전이진트리를 구성하고 있는데, 완전 이진 트리란 모든 노드가 최대 두개 이하의 자식을 가지고 있으며, 왼쪽부터 트리를 채워나가는 형식으로 높이가 h인 트리가 있을 때에 h-1 높이까지 모든 노드는 자식 노드를 두개를 가지고 있고 h의 높이에는 맨 왼쪽부터 노드가 채워지는 구조이다.

또한 힙은 부모 노드와 자식 노드와의 관계가 중요한데. 트리의 모든 노드가 자식보다 같거나 작고, 또는 같거나 커야 하는 구조를 가지게 된다. 최소 힙을 구성하게 될 경우 트리의 모든 노드가 자식보다 같거나 작아야 하며, 최대 힙은 반대가 될 것이다. 이러한 구조를 힙 상태라고 한다.

따라서 이러한 자료구조를 사용하게 되면 항상 Root 노드, 즉 맨 처음 위치의 노드는 항상 최소값이나 최대값이 될 것이다.
이러한 힙 구조를 이용하면 최대값과 최소값을 구하는 데에 트리에서 O(1)의 시간복잡도로 매우 빠르게 구할 수 있을 것이다. 또한 최소 또는 최대힙을 다시 재구성하는 속도도 O(logN)만큼 밖에 시간이 걸리지 않으므로 최소, 최대값을 구하는 데에 매우 빠른 자료 구조라 볼 수 있다.
구현 원리
힙의 구현 원리에 있어 우선 힙은 자신과, 왼쪽 자식, 오른쪽 자식, 부모 노드를 가지게 되는 트리 구조를 이루고, 항상 아까 말한 힙 상태를 유지해야한다.
힙의 추가(Insert)에 있어서는 트리의 맨 마지막 위치에 삽입하여, 해당 힙의 조건에 맞을 때까지 해당 노드의 승격 작업을 반복하게 될 것이다. 만약 최소힙을 만든다고 가정하면 삽입한 위치가 Root가 아닐 때 맨 마지막 위치에 노드를 삽입하고 부모 노드보다 작거나 같으면 바꿔주어 승격 작업을 수행한다. 이러한 과정을 최소힙 상태가 될 때까지 반복하여 해당 노드의 위치를 정해준다.

힙의 삭제(Remove)에 있어서는 힙은 Root 노드의 위치를 반환하고 삭제하는 작업을 수행하는데, Root 노드의 위치의 요소를 반환하고 삭제하고 나면, 트리의 맨 마지막 위치의 노드가 Root 노드가 되며, 그 Root 노드가 해당 힙의 조건에 맞을 때까지 강등 작업을 반복하게 될 것이다. 강등 작업 중 최소 힙에서는 만약 노드가 왼쪽과 오른쪽 자식이 둘다 있다면, 왼쪽 오른쪽 보다 해당 노드가 크다면 더 작은 자식과 교환하고, 왼쪽 자식만 있었다면 해당 노드가 왼쪽 자식보다 더 크다면 왼쪽 자식과 교환하면 된다. 만약 왼쪽 오른쪽 자식 둘다 없었을 경우에는 해당 위치에 두면 될 것이다.
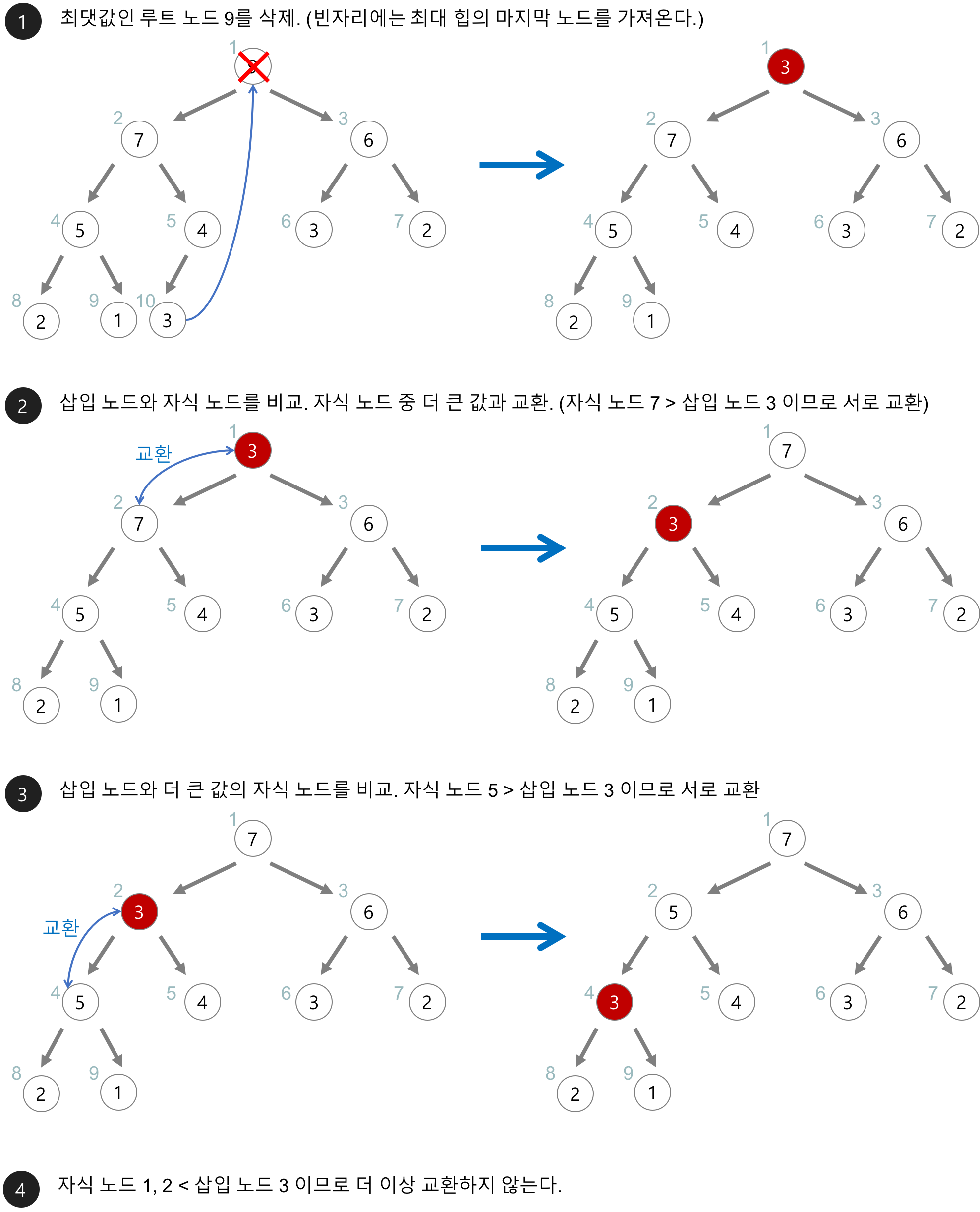
사진 출처 : [자료구조] 힙(heap)이란 - Heee's Development Blog (gmlwjd9405.github.io), 자료구조 - 우선순위 큐(Priority Queue)와 힙(heap) | ChanBLOG (chanhuiseok.github.io)