2023. 10. 16. 23:19ㆍ자료구조, 알고리즘
다익스트라 알고리즘
그래프에서 한 정점으로부터 모든 정점으로의 최단거리의 경로를 구하는 알고리즘
1. 지금 연결되어 있는 노드 중에서 탐색을 안한 노드중 가장 가까운 노드를 선정한다.
2. 직접 연결된 거리보다 거쳐서 더 짧아지면 갱신한다.
3. 이 과정을 반복하다보면 최단 경로가 나온다.
예시
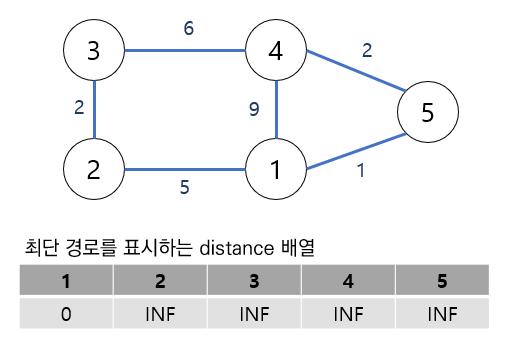
1번 정점에서 시작해서 모든 정점들까지의 최단 경로를 구한다고 가정해 보겠습니다.
정점들 간의 간선의 가중치는 그림과 같고, distance 배열은 1번 정점에서 특정 정점까지의 최단 경로 길이를 표시해 놓습니다.
단, 초기에는 최단 경로를 구하지 않은 상태이므로 무한대(아주 큰 값)로 표시합니다.
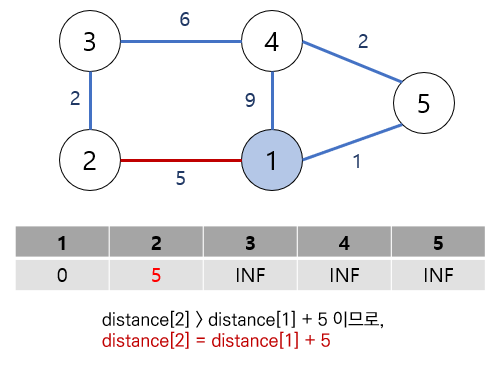
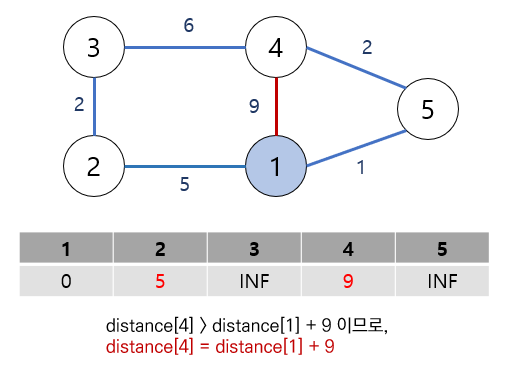
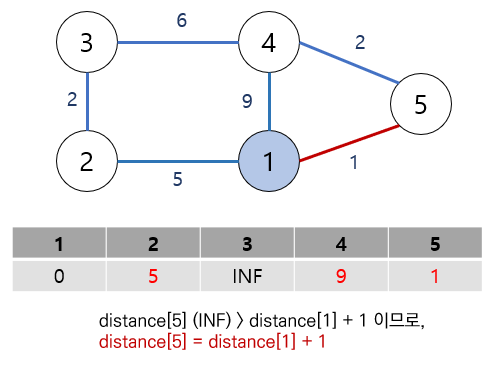
1번 정점에서 인접한 정점들을 살펴봅니다.
처음에는 모두 무한대 값들이었으므로, 1번 — 특정 정점 까지의 간선 가중치로 모두 업데이트가 될 것입니다.
즉, distance[특정 정점] 과 distance[1] + (1번 정점과 특정 정점 사이 가중치) 를 비교해 더 작은 값으로 distance[특정 정점] 을 업데이트합니다.
이것이 다익스트라 알고리즘의 핵심 과정이자 전부라고 할 수 있습니다.
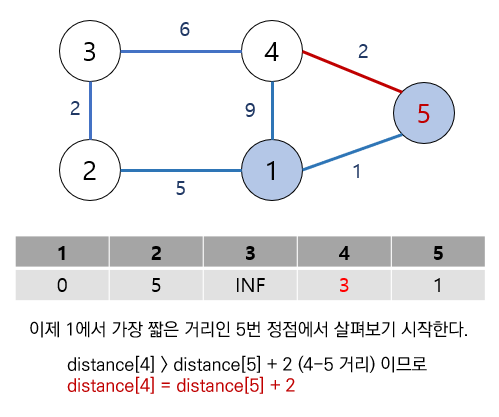
이제 5번 정점에서 인접 정점을 살펴봅니다. 1번은 이미 처리했으므로, 4번 정점과의 거리만 살펴봅니다.
distance[4] 값은 1에서 바로 4로 갈 때의 거리인 9 였는데, 5번 정점에서 살펴보니, 1번에서 5번을 거쳐(distance[5]), 4번으로 가는 경로(5와 4 사이 가중치) 가 더 짧음을 알 수 있습니다.
출처 : 알고리즘 - 다익스트라 알고리즘(Dijkstra's algorithm) : 모든 정점까지의 최단 경로 구하기 | ChanBLOG (chanhuiseok.github.io)
A* 알고리즘
다익스트라 알고리즘을 확장하여 만든 최단 경로 탐색알고리즘으로
탐색의 우선순위를 두고 유망한 해부터 우선적으로 탐색한다, 우선 순위 큐를 사용한다.
1. 탐색하지 않은 가장 유망한 해를 선정하여
2. 그 곳을 거쳐 더 짧아 지는 경로로 대체한다.
f, g, h 점수를 계산하여 조금 더 유망한 경로부터 우선 탐색
(h : 예상 거리, g : 지금까지 온 거리, f : 총 소요 거리)
h(휴리스틱)에 따라서 알고리즘의 효율이 달라짐
1. f 점수가 가장 낮은 정점부터 선정
2. 그 정점을 기준으로 탐색 가능한 정점들의 f 점수를 구해줌
f 총 소요 점수 : g + h

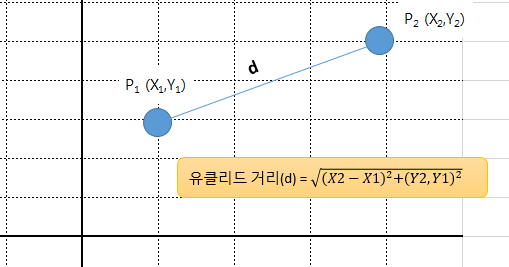
휴리스틱 - 맨해튼 거리 vs 유클리드 거리
유망한 해에 대한 선정기준으로 맨해튼 거리법과, 유클리드 거리법이 있는데 맨해튼 방식으로는 시작 위치부터 목적지 위치까지 대각선을 고려하지 않고 갈 수 있는 모든 거리이며 유클리드 방식은 시작 위치부터 목적지까지의 갈 수 있는 대각선 거리를 고려한 방식이다.

'자료구조, 알고리즘' 카테고리의 다른 글
| 탐색 알고리즘 (0) | 2023.10.16 |
|---|---|
| 정렬 알고리즘 (0) | 2023.10.11 |
| 해시테이블 (0) | 2023.10.10 |
| 이진탐색트리 (0) | 2023.10.09 |
| 우선순위 큐 - Heap (0) | 2023.10.08 |